Eine Schusslösung berechnen

Artilleriecomputer

Mit einem Artilleriecomputer, wie ihn moderne Systeme auch in der Realität besitzen und wie er in Arma für alle Artillerietypen verfügbar ist, lässt sich die Schusslösung automatisch berechnen und direkt in eine korrekte Ausrichtung der Waffe umsetzen. Der Ablauf ist einfach:

1. Der Schütze öffnet den Artilleriecomputer und wählt die gewünschte Munitionsart aus.
2. Auf der Karte klickt der Schütze die Zielkoordinate an und wechselt ggf. die Ladungen (mehr Ladungen bedeuten mehr Reichweite).
3. Sobald die richtige Munition geladen und die Kanone ausgerichtet ist, feuert der Schütze durch einen Klick auf die entsprechende Schaltfläche.

Der Missionsbauer kann den Artilleriecomputer für bestimmte oder alle Geschütze in einer Mission deaktivieren. Dann müssen die Schützen die Ausrichtung des Geschützes selbst berechnen. Dazu sind dann drei Werte zu berechnen:

• der horizontale Winkel, auch Azimuth,
• die Entfernung zum Ziel und
• die Einstellung der Höhe des Rohres, englisch Elevation.

Gegeben sein müssen die folgenden Werte:

• die Position des Ziels in einem Koordinatensystem, einschließlich der Höhe,
• die eigene Position in einem Koordinatensystem, einschließlich der Höhe.

Wie Positionen bestimmt werden können, wird im Artikel Orientierung im Gelände erläutert.

Entfernung bestimmen

In Arma lässt sich die Entfernung zwischen zwei Punkten leicht durch den Satz des Pythagoras bestimmen: Das Quadrat der Entfernung (d) zum Ziel ist gleich dem Quadrat der Differenz auf der y-Achse (dy) plus dem Quadrat der Differenz auf der x-Achse (dx). Gehe wie folgt vor:

1. Ergänze zunächst alle Koordinaten zu fünfstelligen (auf den Meter genau). Hänge ggf. einfach Nullen an.
2. Substrahiere nun von der x-Koordinate des Ziels deine eigene x-Koordinate. Behalte ein negatives Vorzeichen bei! Notiere dir diesen Wert als „Differenz x“ oder kurz dx.
3. Wiederhole das gleiche für die y-Koordinaten.
4. Berechne nun mit dem Satz des Pytagoras die Distanz d:

$d{ }^2=\hspace{0.17em}d{x}^2 + d{y}^2$

$d = \sqrt{d{x}^2 + d{y}^2}$

Notiere dir diese Werte, da du sie auch für die folgende Rechnung benötigst!

Einfacher lässt sich die Entfernung mit Hilfsmitteln ermitteln:

• Mit dem ACE Kartenwerkzeug lässt sie sich wie mit einem Lineal ablesen.
• Mit einem ACE MicroDAGR lässt sie sich ermitteln, indem man die Zielkoordinate als Wegpunkt setzt und dann die Entfernung zum aktuellen Wegpunkt abliest.

Azimuth bestimmen

Auch der Winkel zum Ziel lässt sich errechnen. Da wir den Winkel in MIL benötigen, müssen wir ihn vom Bogenmaß in MIL umrechnen. Dazu muss dein Taschenrechner im Bogenmaß (rad) eingestellt sein. Die benötigten Werte d und dy behalten wir aus der vorangegangenen Rechnung bei.

Da die Arkkosinusfunktion immer den kleineren Winkel ergibt (zwischen 0° und 180°) müssen wir das Ergebnis korrigieren, wenn das Ziel westlich liegt (also zwischen 180° und 360°). Dazu substrahieren wir das Ergebnis von einem vollen Winkel (6400 MIL).

Die Berechnung erfolgt also nach einem der beiden Fälle:

Normale Karten
Ziel östlich	$1019 \times {{\cos }_r}^{-1}\left(\frac{dy}{d}\right)$
Ziel westlich	$6400 - 1019 \times {{\cos }_r}^{-1}\left(\frac{dy}{d}\right)$

Auf einigen Karten ist allerdings das Koordinatensystem auf der y-Achse verkehrt: Die Position 00000-00000 ist dort nicht im Südwesten, sondern im Nordwesten der Karte (das gilt bspw. für Chernarus). Dann muss vom Wert dy einfach das negative Gegenstück gewählt werden.

„Verkehrte“ Karten
Ziel östlich	$1019 \times {{\cos }_r}^{-1}\left(\frac{-dy}{d}\right)$
Ziel westlich	$6400 - 1019 \times {{\cos }_r}^{-1}\left(\frac{-dy}{d}\right)$

Alternativ lässt sich die Azimuth auch mit Hilfsmitteln bestimmen:

• Wenn das Ziel in Sichtweite ist, lies die Azimuth am Kompass ab. Dieser verfügt über eine äußere Skala (0-64), deren Wert mit 100 multipliziert werden muss, um MIL zu ergeben.
• Die gleiche Skala ist auch auf dem ACE Kartenwerkzeug zu finden, sodass der Wert von der Karte abgelesen werden kann.
• Wenn du die Entfernung wie oben beschrieben mit dem MicroDAGR bestimmt hast, kannst du damit auch den Winkel zum Ziel ermitteln. Schalte zunächst in den Einstellungen des MicroDAGRs die Winkeleinheit auf MIL um. Lies anschließend den Winkel im Hauptbildschirm ab.

Elevation

Die Höheneinstellung gibt den Winkel vor, in dem das Geschoss seine Flugbahn beginnt. Dieser Winkel muss an drei Faktoren angepasst werden:

• die verwendete Treibladung,
• die Entfernung zum Ziel,
• die Differenz der Höhe zwischen Abschussort und Ziel.

Diese Werte lassen sich mit der Rangetable und etwas Rechnerei schnell ermitteln.

Rangetable und Treibladung

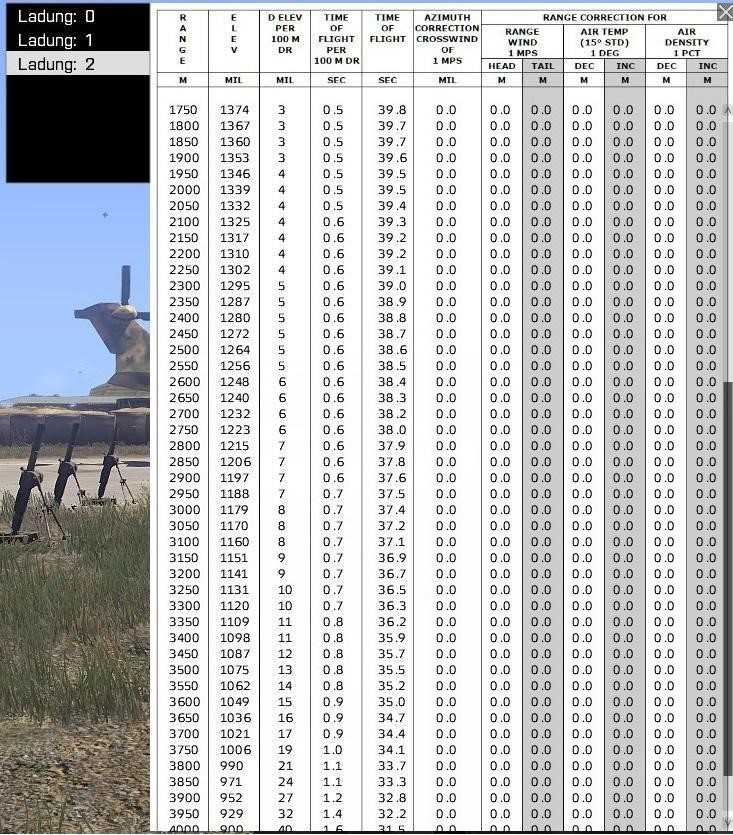
Anhand dieser Werte lässt sich die einzustellende Elevation in einer Rangetable ablesen (vgl. Bild rechts). Diese enthält die folgenden Informationen:

Eigenschaft	Einheit	Beschreibung
Range	Meter	Die Entfernung zum Ziel.
Elev.	MIL	Für die Entfernung einzustellende Höhe
D Elev. per 100m dr.	MIL	Pro 100 Meter Höhendifferenz vorzunehmende Korrektur der Elevation
Time of flight per 100m dr	Sekunden	Differenz der Flugzeit pro 100 Meter Höhendifferenz
Time of flight	Sekunden	Flugzeit des Geschosses

Alle übrigen Werte werden bei den Einstellungen von Gruppe W nicht benötigt.

Die Treibladung (engl. Charge) kann vom Schützen festgelegt werden. Dabei handelt es sich um zusätzliche Ladungen, die ans Geschoss angebracht werden und dadurch die Mündungsgeschwindigkeit erhöhen. Eine höhere Mündungsgeschwindigkeit bewirkt eine höhere Reichweite. Daher hat die Rangetable mehrere Seiten. Wähle die Treibladung so, dass die dir bereits bekannte Entfernung im niedrigen oder mittleren Bereich der Entfernungswerte auftaucht, da die Zielgenauigkeit am oberen Grenzwert abnimmt.

Elevation berechnen

Die Elevation wird nun anhand der Entfernungsangaben ermittelt. Da die exakte Entfernung nicht in der Tabelle aufgeführt ist, muss sie abgeschätzt oder berechnet werden. Die Berechnung erfolgt nach folgender Formel:

1. Ermittle die jeweils höhere und geringere Entfernung, die in der Rangetable auftaucht:
   Beispielentfernung: $2980m$
   Kleinerer Wert: $2950m$ und $1188mil$
   Größerer Wert: $3000m$ und $1179mil$
2. Berechne die Differenz zwischen den Elevation-Angaben der beiden Werte:
   $1188mil - 1179mil =\hspace{0.17em}9mil$
3. Ermittle mit einem Dreisatz die MIL-Differenz vom kleineren Wert:
   $2980m - 2950m =\hspace{0.17em}30m$
   $\frac{50m}{30m}\times 9mii =\hspace{0.17em}5,4 mil$
4. Substrahiere diesen Wert von der MIL-Angabe für die kürzere Entfernung, um die einzustellende Elevation zu erhalten:
   $1188mil - 5,4mil =\hspace{0.17em}1182,6mil$

Zusammengefasst:

$el =\hspace{0.17em}e{l}_k - \frac{\left(e{l}_k-e{l}_g\right) \times \left(d-d_k\right)}{50m}$

(el: Elevation; d: Distanz; k: kürzere Distanz; g: größere Distanz)

Höhenkorrektur berechnen

Die Flugkurve muss angepasst werden, wenn das Ziel höher oder tiefer liegt, als der Schütze. Gehe wie folgt vor:

1. Ermittle die Höhe des Ziels und deiner eigenen Position mithilfe der Karte oder eines Höhenmessers. Berechne nun die Differenz zwischen beiden Höhen.
2. Ermittle den Korrekturwert aus der Rangetable abhängig von der Entfernung. Dieser kann abgeschätzt oder ähnlich wie die Elevation berechnet werden.
3. Multipliziere MIL-Angabe pro 100m und Höhendifferenz.

$Korrektur =\hspace{0.17em}\left(h_{Schütze}-h_{Ziel}\right)\times \frac{x MIL}{100m}$

Das Ergebnis wird nun zur Elevation addiert (Vorzeichen beachten!). Je höher das Ziel im Vergleich zum Schützen, desto geringer die Elevation.

BalMAR

Ein mögliches Tool zur schnellen halbautomatischen Berechnung der Schusslösung ist das Tool BalMAR. BalMAR steht für Balistischer Mörser und Artillerie Rechner und ermittelt mittels Pythagoras und Trigonometrie die passende Treibladung, Entfernung, Flugdauer, Winkel und Elevation. Hinter diesem Tool steckt ein Programm auf Basis von Microsoft Excel in Kombination mit VBA-Programmierung.

Dieser Rechner kann mittels Koordinaten präzise die Zieleinstellungen für jegliches Steilgeschütz berechnen. Eine Berechnung ist für einen Punkt-, Flächen- oder einen Linien-Angriff möglich.

▶ DOWNLOAD und weitere Informationen

Generell gilt jedoch:

• Ein externer Mörser-Rechner sollte nicht genutzt werden, wenn Arma dafür runtergeklickt werden muss.
• Besser als das Berechnen der Schusslösung ist immer das Feuer auf Sicht, da man hier innerhalb von wenigen Sekunden feuerbereit ist.

Spezialfall: Feuer auf Sicht oder sehr kurze Distanz

Feuer auf Sicht liegt vor, wenn der Schütze das Ziel sehen kann. Dies ermöglicht schnellere Reaktionszeiten, birgt aber auch Risiken, da meist umgekehrt auch das Ziel den Schützen sieht.

Die meisten Berechnungen können in dem Fall ausgelassen werden. Gehe stattdessen wie folgt vor:

1. Stelle das Geschütz so auf, dass das Ziel im Sichtwinkel liegt.
2. Nimm das Ziel ins Visier des Geschützes.
3. Miss die Entfernung entweder mit einem integrierten Entfernungsmesser oder lass sie von einem Assistenten mit Entfernungsmesser oder Schätzung bestimmen.
4. Stelle die Elevation gemäß Rangetable ein. Schätze Zwischenwerte ab. (Im Einsatz an der Frontlinie kann diese Tabelle hilfreich sein.)
5. Feuere und beobachte den Einschlag bzw. lass einen Assistenten diesen beobachten. Korrigiere die Einstellungen entsprechend. Durch die kurze Flugzeit lassen sich Korrekturen oft schon für den nächsten Schuss übernehmen.